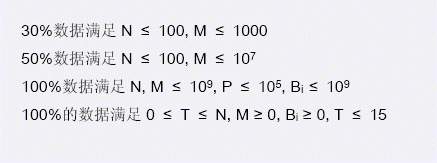Gate Of Babylon

Time Limit: 10 Sec Memory Limit: 162 MB

Description

img

Input

img

Output

img

Sample Input

2 1 10 13

3

Sample Output

12
　　img

HINT

img

Main idea

有若干个没有限制的道具，以及T个有限制个数的道具，取出m个，求方案数。

Solution

首先，看到有限制的只有15个，因此可以考虑使用容斥原理：Ans=全部没有限制的方案-有1个超过限制的方案数+有2个超过限制的方案数-有3个超过限制的方案数…。

以此类推。我们先考虑没有限制的，在m组无限制的数中选n个的方案数，显然就是C(n+m-1,n)。

因为这道题是要求不超过m的方案数，也就是那么运用加法原理，发现答案也就是C(n+0-1,0)+C(n+1-1,1)+C(n+2-1,2)+…+C(n+m-1,m)=C(n+m,m)。

然后考虑有限制的情况，有一个超过限制直接用总数减去（这个的限制+1)就是当前的总数，相当于强制要选限制+1个为空。

然后只要DFS，记录到当前为止选了几个，答案要记是b[i]+1,判断加减，最后累加答案。

最后，n、m过大，发现p是一个质数，所以可以用Lucas定理：Lucas(n,m,p)=Lucas(n/p,m/p,p)*C(n%p,m%p)，其中C(n%p,m%p)求的时候要用到乘法逆元。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
#include<bits/stdc++.h>
using namespace std;

const int ONE=1000001;

int n,T,m,MOD;
long long Ans;
long long Jc[ONE];
int b[ONE];

int get()
{
    int res,Q=1;    char c;
    while( (c=getchar())<48 || c>57)
        if(c=='-')Q=-1;
    if(Q) res=c-48;
    while((c=getchar())>=48 && c<=57)
        res=res*10+c-48;
    return res*Q;
}

long long Quickpow(int a,int b,int MOD)
{
    long long res=1;
    while(b)
    {
        if(b&1) res=res*a%MOD;
        a=(long long)a*a%MOD;
        b/=2;
    }
    return res;
}

int C(int m,int n)
{
    if(m<n) return 0;
    int up=Jc[m]%MOD;
    int down=(long long)Jc[m-n]*Jc[n]%MOD;
    return (long long)up*Quickpow(down,MOD-2,MOD)%MOD;
}

int Lucas(int n,int m,int MOD)
{
    long long res=1;
    if(n<m) return 0;
    while(n && m)
    {
        res=res*C(n%MOD,m%MOD)%MOD;
        n/=MOD; m/=MOD;
    }
    return res;
}

void Dfs(int len,int PD,int val)
{
    if(len==T+1)
    {
        Ans+=PD*Lucas(n+m-val,m-val,MOD);
        Ans+=MOD;
        Ans%=MOD;
        return;
    }
    Dfs(len+1,PD,val);
    Dfs(len+1,-PD,val+b[len]+1);
}

int main()
{
    n=get();    T=get();    m=get();    MOD=get();
    Jc[0]=1; for(int i=1;i<=MOD;i++) Jc[i]=(long long)Jc[i-1]*i%MOD;
    for(int i=1;i<=T;i++)
        b[i]=get();
    Dfs(1,1,0);
    printf("%d",Ans);
}